离散数学课(CSCI 2110)上,讲到一个有趣的问题。
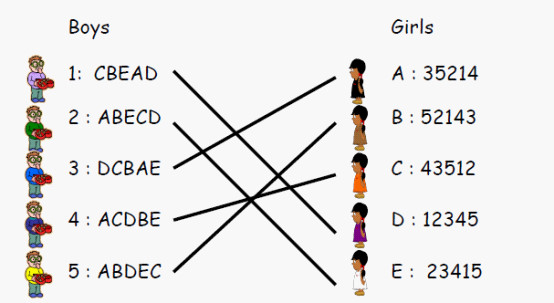
假设有五个男生,五个女生,每个人都在自己心中对五个异性有一定的preference排序,比如:
以上的排序表解读为:男生1最中意女生C,次中意女生B,次次中意女生E。。。。 以此类推。。。。
在五男五女全部成功脱光之后(假设都在圈子内部解决),定义一个unstable matching为:如果存在一对不是情侣的男女符合以下情况:
对于该男,该女在他的preference列表中处于现任女友的前面,对于该女,该男在他的preference列表中亦处于现任男友的前面,那么这对男女必然有私奔的倾向。。。。
这样的情景即为unstable matching。反之,若不存在这样一对有私奔倾向的男女,即为stable matching。
问题是:是否在任何情况下,即不论各位的preference列表如何变化,只要男女数量相同,总是存在一个stable matching。? (当然,搅基之类的,是不可以的。。。)
在上面五男五女的例子里,一种stable matching如下:
因为每个女生最中意的男生都不同,所以只要让女生们都选择跟自己最中意的男生在一起,她们就都不会有和其他男生私奔的想法。虽然男生们会表示略苦逼啊!仍然不失为一个stable matching。。。。。
那么如果有n男n女,每个人心中都已经有了一个preference 列表,stable matching是不是一定存在呢?
1962年,Gale 和 Shapley 证明了stable matching是一定存在的。
首先他们给出了一个算法:
第一天早上:所有男生都向自己最中意的女生表白。
第一天中午:每个女生都被表白了n次(可能是0次)之后,拒绝了相对不太中意的那n-1位,hold住其中最中意的那位。。。即暂时不答应也不拒绝
第一天晚上,被拒绝的男生们在自己的preference列表中划掉了那个拒绝他的人。。。
第二天早上:所有没有被hold住的男生都向自己最中意的女生(无视已经被划掉的)表白。
第二天中午:女生们在那些向她表白的男生和已经hold住的那男生中选择最中意的一位,拒绝掉其他的。
第二天晚上:被拒绝的男生们在自己的preference列表中划掉拒绝了自己的人。。。。
第三天,重复同样的过程。。。
第四天。。。。
这样的过程是有限的,不会一直循环下去。(Claim 1)
在这样的过程结束之后,每个女生都会hold住一个男生。(Claim 2)即在那一天之后没有男生可以继续表白了,这时女生们终于都向那个男生说了yes!
按照这样的过程,最后不会存在一对男女有私奔倾向(Claim3)
即完成了stable matching。
关于Claim1, Claim2, Claim3的证明,有兴趣的同学可以参考这里:http://en.wikipedia.org/wiki/Stable_marriage_problem#Solution
下面是我们的关键问题:
在这样男生主动的算法中,占了优势的是男生还是女生呢?
表面上,男生略苦逼:要么被拒绝,要么被hold住还不知道是不是第二天就会被拒绝;女生则有着充分的选择权,享受着众星捧月的优越感,而且最差情况下到头来还是会有个伴儿也不至于孤家寡人。。。。。。
但是实际上,占了优势的却是男生!
对于男生,设最后他的女友是在他当初的preference列表的第i位,那么在i位之前的那些女生,他是怎么追也追不到的:因为即使追到(即该女生一时糊涂答应了),那么那个女生(记为Y)也必然会有比他心仪的对象另一男X(因为既然是一时糊涂,表明在当时的情况下有更心仪的男生已经向她表白),而男X既然在当时向该女生表白,表明在Y之前的女生都拒绝了他,而如果Y也拒绝了他,他最后在一起的女生必定排在Y之后。
所以,X和Y是注定要私奔的!
所以嘛,男生没有追到的那些女生,都是命中不该有不可强求的。。。即他最后追到的女生是他最好的选择了。。。
对于女生:
设最后她的男友在她当初的preference列表的第i位,那么在i位之前的那些男生,都是还没机会向她表白就被其他女生hold住的,也就是说,她永远也等不到的最好的,多苦啊。。。
实际上,还可以证明,这个男友是在所有的stable matching中她能得到的最差的选择。
如果她选择了i+1,也就是拒绝了i,那么i最后只能跟不如她的女生(在i眼中)在一起。而i+1也是不如i的,那么最后她还是要和i私奔。
即:若她选择了(在她眼中的)更差的男生,最后的配对就是unstable matching了,所以,没办法更差了!这已经是最差了有木有啊!
综上,我们惊奇地发现,男生追到的女生,是他最好的选择。
女生接受的男生,是她最差的选择。
如果情况相反,即女生主动追求男生,那么结论也会相反。
这个事实教导我们,主动表白是多么重要啊!
但是。。。。
羞涩的女生如果不愿主动表白,还是有机会避免这种最差结果的。这时候,撒点小谎就显得非常重要。。。。。
假设一个简单的情境,4 V 4 好了。
男1:BADC A女:1234
男2:ABCD B女:2143(红色是在第一天表白的)
男3:BCAD C女:3241
男4:ADBD D女:4231
按照Gale Shapley算法:
第一天,男1和男3向B女表白,男2和男4向A女表白。
A女喜欢2胜过喜欢4,但是她对2说谎了(“不,我不爱你。。。”)她拒绝了2
B女喜欢1胜过喜欢3,但是她对1说谎了,她拒绝了1
于是第二天早上,被拒的男1向A女表白,同时男2向B女表白。。。。。。
最后的结果是:
1-A
2-B
3-C
4-D
女生们最终都得到了最佳选择。
以上的事实教导我们,当女生拒绝你的时候,可能她不是真的不喜欢你(至少在当时),所以。。。一切死缠烂打都是有理论依据滴,不可等同于耍流氓。。。。
最后,如果是男生撒谎(即不按preference列表来表白,不能否认这样的2B青年的存在),他最终能不能交到更加心仪的女友呢?答案是不能。撒谎只会让男生交到在男生心目中排得更靠后的女生。原因不难分析,同学们可以自行尝试。结论是:对于主动的一方,真诚和坦白是保证得到最优选所必需的。。。

感性思考也不难理解为什么男生比女生占优,因为男生一开始就能从最好的开始挑,而女生并不能。
得留下个脚印,以后要常来看看。
海量数据 搜索等等
原来ITmian.com也是你的站啊。。
学习