【什么是Hash】
Hash,一般翻译做“散列”,也有直接音译为“哈希”的,就是把任意长度的输入(又叫做预映射, pre-image),通过散列算法,变换成固定长度的输出,该输出就是散列值。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,而不可能从散列值来唯一的确定输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。
HASH主要用于信息安全领域中加密算法,它把一些不同长度的信息转化成杂乱的128位的编码,这些编码值叫做HASH值. 也可以说,hash就是找到一种数据内容和数据存放地址之间的映射关系。
数组的特点是:寻址容易,插入和删除困难;而链表的特点是:寻址困难,插入和删除容易。那么我们能不能综合两者的特性,做出一种寻址容易,插入删除也容易的数据结构?答案是肯定的,这就是我们要提起的哈希表,哈希表有多种不同的实现方法,我接下来解释的是最常用的一种方法——拉链法,我们可以理解为“链表的数组”,如图:
左边很明显是个数组,数组的每个成员包括一个指针,指向一个链表的头,当然这个链表可能为空,也可能元素很多。我们根据元素的一些特征把元素分配到不同的链表中去,也是根据这些特征,找到正确的链表,再从链表中找出这个元素。
元素特征转变为数组下标的方法就是散列法。散列法当然不止一种,下面列出三种比较常用的。
1,除法散列法
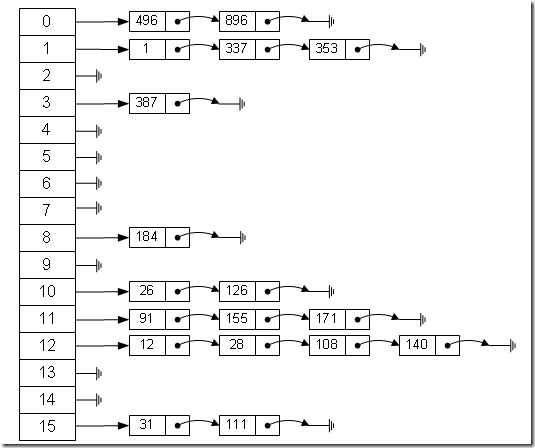
最直观的一种,上图使用的就是这种散列法,公式:
index = value % 16
学过汇编的都知道,求模数其实是通过一个除法运算得到的,所以叫“除法散列法”。
2,平方散列法
求index是非常频繁的操作,而乘法的运算要比除法来得省时(对现在的CPU来说,估计我们感觉不出来),所以我们考虑把除法换成乘法和一个位移操作。公式:
index = (value * value) >> 28
如果数值分配比较均匀的话这种方法能得到不错的结果,但我上面画的那个图的各个元素的值算出来的index都是0——非常失败。也许你还有个问题,value如果很大,value * value不会溢出吗?答案是会的,但我们这个乘法不关心溢出,因为我们根本不是为了获取相乘结果,而是为了获取index。
3,斐波那契(Fibonacci)散列法
平方散列法的缺点是显而易见的,所以我们能不能找出一个理想的乘数,而不是拿value本身当作乘数呢?答案是肯定的。
1,对于16位整数而言,这个乘数是40503
2,对于32位整数而言,这个乘数是2654435769
3,对于64位整数而言,这个乘数是11400714819323198485
这几个“理想乘数”是如何得出来的呢?这跟一个法则有关,叫黄金分割法则,而描述黄金分割法则的最经典表达式无疑就是著名的斐波那契数列,如果你还有兴趣,就到网上查找一下“斐波那契数列”等关键字,我数学水平有限,不知道怎么描述清楚为什么,另外斐波那契数列的值居然和太阳系八大行星的轨道半径的比例出奇吻合,很神奇,对么?
对我们常见的32位整数而言,公式:
i ndex = (value * 2654435769) >> 28
如果用这种斐波那契散列法的话,那我上面的图就变成这样了:
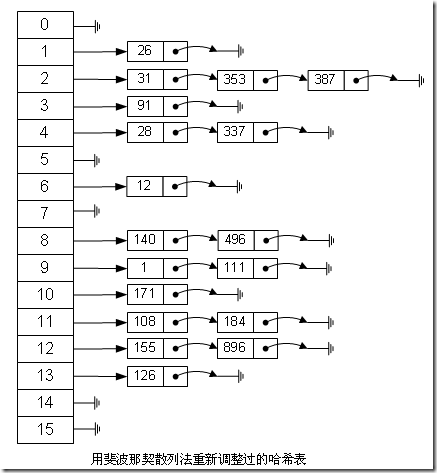
很明显,用斐波那契散列法调整之后要比原来的取摸散列法好很多。
【适用范围】
快速查找,删除的基本数据结构,通常需要总数据量可以放入内存。
【基本原理及要点】
hash函数选择,针对字符串,整数,排列,具体相应的hash方法。
碰撞处理,一种是open hashing,也称为拉链法;另一种就是closed hashing,也称开地址法,opened addressing。
【扩展】
d-left hashing中的d是多个的意思,我们先简化这个问题,看一看2-left hashing。2-left hashing指的是将一个哈希表分成长度相等的两半,分别叫做T1和T2,给T1和T2分别配备一个哈希函数,h1和h2。在存储一个新的key时,同 时用两个哈希函数进行计算,得出两个地址h1[key]和h2[key]。这时需要检查T1中的h1[key]位置和T2中的h2[key]位置,哪一个 位置已经存储的(有碰撞的)key比较多,然后将新key存储在负载少的位置。如果两边一样多,比如两个位置都为空或者都存储了一个key,就把新key 存储在左边的T1子表中,2-left也由此而来。在查找一个key时,必须进行两次hash,同时查找两个位置。
【问题实例】
1).海量日志数据,提取出某日访问百度次数最多的那个IP。
IP的数目还是有限的,最多2^32个,所以可以考虑使用hash将ip直接存入内存,然后进行统计。
做人要厚道,转载请注明出处: http://diducoder.com/mass-data-topic-3-hash.html
我觉得好深奥,都看不懂,是什么东西?我改怎么办,有什么方法可以让我看懂啊?楼主
[quote]我觉得好深奥,都看不懂,是什么东西?我改怎么办,有什么方法可以让我看懂啊?楼主[/quote]
可以先复习下数据结构方面的东西,然后再看就不吃力啦~~~
我想知道斐波那契(Fibonacci)散列法一定是>>28么?为什么选择了28呢?
TO toraleap: 这个当然不是了,只是这个例子中需要>>28,因为左边是数组有16个位,所以需要0-15的哈希值,所以右移28位就只剩4位,所以右移后的值域刚好是【0,15】
问题实例能不能详细点解释下?
谢谢分享
不是很深吧!看看数据结构的书就能明白了
现在看不到文章中的图片了,能补上么。
我最近在看你的《海量数据处理专题》写的蛮好,赞一个。
最近换了博客系统,所以图片都丢失了,我会抽时间把这些图片补上。谢谢支持
对于存储手机号或者imei号,用什么hash函数比较合适?让其散列的比较均匀?
这个问题很值得讨论,首先是你采用什么数据类型来存储手机号,如果是用数值型,那么理论上手机号码是随机分布,因此最简单的取摸就可以保证散列均匀,(当然了,int型数值是不能存放完整手机号,因此可以采用多级hash的方法,这就有点类似于trie树,但是和trie树还是有本质区别)。如果采用字符串型,那么普通的MD5,SHA1都是可选的方法,另外,trie树的结构效率也是很高的,而且不存在碰撞问题。本系列后面的文章会讲到Trie树的结构。
谢谢!其实我要存储手机号或者imei代码是为压缩内存占用空间的,md5后会更占空间了。有没有别的hash函数可以大大压缩呢?
其实时间和空间是相对的,如果要压缩空间,那么时间复杂度就会相应的提高。在您的这个例子中,如果一点要通过hash函数(例如用取摸法的时候用比较小的数)压缩,那么左边的数组会变小(桶容量),但是后面的拉链会比较长,也就是说,碰撞的概率会变大。
您可以分析您的数据分布特征,找到合适的hash方法。
好的,我试试,多谢!
我觉得手机号的后四位就可以作为hash了,至于IMEI,它的编码形式不大懂,选择一段随机位作为index就可以了。
还有楼主上面提到的2d-left hash方法,是为了改进false positive rate还是为了保持每个每个碰撞的list保持相对一致的长度?
使用手机号后四位,发生碰撞的概率太大了,反而效率不高。
引用通告: 海量数据处理专题(一)——开篇 | 帝都码农